
My work explores the practical aspects of how bound, stored, or static electromagnetic energy transforms into moving electromagnetic energy. I’ve applied this expertise in the design of ultra-wideband (UWB) antennas, as well as in wireless systems that operate using near-field wireless principles. Q-Track designs indoor location systems that locate tags to typical accuracies better than 50cm and typical ranges of 50m or less. Operating at around 1MHz with wavelengths of 300m, these systems exploit the physical properties of radio waves precisely as they are born. Everyday, my Q-Track colleagues and I engineer with the fundamental physics of photon emission and absorption scaled up to macroscopic size. This practical experience yields interesting insights to electromagnetic behavior with, I believe, deep relevance to fundamental physics.
Today’s blog post applies and explains some of my recent work on near-field electromagnetic physics. I examine a basic confusion in quantum mechanics regarding interference and show how those same issues play out in the interactions between radio waves on the macroscopic scale. Classical electromagnetics teaches valuable lessons about how the quantum world must behave. After all, the correspondence principle of quantum mechanics tells us that quantum physics converges to classical behavior in the limit. The conclusions – concepts like EM energy bouncing elastically in free space – are both surprising and deeply counter-intuitive. These conclusions require no new physics, merely the rigorous application of the superposition principle to the time-tested teachings of Maxwell, as refined and made latent by his successors like Heaviside, Poynting, Lodge, and Schelkunoff.
Let’s begin by taking a look at what quantum mechanics has to say about the interference or interaction of electromagnetic waves.
Quantum Interference
Paul A.M. Dirac (1902-1984) made fundamental contributions to quantum mechanics and quantum electrodynamics. He was a respected arbiter on quantum theory and its meaning. Feynman quipped that physicists all read Schiff (a leading graduate text book), but they all quote Dirac. Here’s how Dirac explained interference on a quantum level:

“Suppose we have a beam of light consisting of a large number of photons split up into two components of equal intensity. On the assumption that the intensity of this beam is connected with the probable number of photons in it, we should have half the total number of photons going into each component. If the two components are now made to interfere, we should require a photon in one component to be able to interfere with one in the other. Sometimes these two photons would have to annihilate one another, and other times they would have to produce four photons. This would contradict the law of conservation of energy. The new theory, which connects the wave function with probabilities for one photon, gets over the difficulty by making each photon go partly into each of the two components. Each photon then interferes only with itself. Interference between two different photons never occurs.” P.A.M. Dirac, The Principles of Quantum Mechanics, 4th ed. (revised), 1967, p. 9.
The energy of a field goes as the square of the field. Doubling the field intensity yields four times the energy. If the field intensity is zero, so also is the energy.
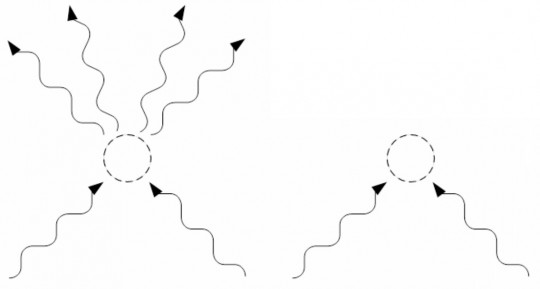
If two photons interfere constructively, their fields add together linearly to yield twice the field intensity. But that would mean four times the energy, or in other words, two photons interacting to yield four. If two photons interfere destructively, their fields cancel out, as do their energies. But that implies that two photons destructively interfere to yield none. Either result, depicted in the figure above, violates conservation of energy. Thus, in Dirac’s view, conservation of energy requires that photons can never interfere with each other, only with themselves.
It turns out, I’m hardly the first to express skepticism with Dirac’s claim. The Skulls in the Stars blog has a great description of quantum optics experiments that disprove Dirac’s argument (H/T to Travis Norsen for bringing this to my attention). This blog post describes an experiment by Magyar and Mandel in which interference fringes from two independent lasers were observed.
Classical EM Interference
What does classical electromagnetics have to say about energy conservation when electromagnetic waves interfere?
Consider two elemental waves under constructive interference. We may imagine these waves comprising unit electric (E) and magnetic (H) fields orthogonal to each other. The fields are transverse or orthogonal to the direction of travel given by the Poynting vector (S = E x H). The right-handed sense of E to H with respect to S is critical for understanding how waves interact with each other. Constructive interference is the co-parallel alignment of the electric field vectors. Assuming unit fields, this doubles the electric field intensity and yields four times the energy. We end up with more electric energy than that with which we started. But interference does not violate the law of conservation of energy. Interference merely converts one form of energy to another. Due to the right-handed sense of the fields described by the Poynting vector, when the E-fields align constructively in a head-on collision, the H-fields align destructively. Where we started with unit magnetic energy in each elemental wave, we now have no magnetic energy. The original magnetic energy has transformed entirely to electric energy. Conservation of total energy holds. The figure below illustrates how this works for constructive interference (left).
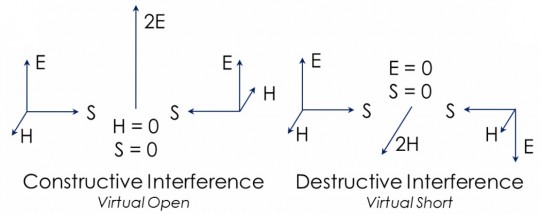
Destructive interference works similarly. In destructive interference, the electric fields cancel and the magnetic fields add constructively. The original balance of electric and magnetic energy present in the two propagating waves converts entirely to magnetic energy at the moment of destructive interference. Again, total energy is conserved. Princeton physics professor Kirk McDonald offers an excellent analysis (“Does Destructive Interference Destroy Energy?“).
And thus, the nature of Dirac’s big mistake becomes obvious by reference to classical EM. Dirac implicitly assumed that photons were the quantized energy of a single field. Instead, they are the quantized energy of two closely coupled and related fields: electric and magnetic. This dual nature of electromagnetic fields means that electromagnetic waves can and do interact constructively or destructively without violation of the law of conservation of energy.
But these transformations of energy between electric and magnetic forms have additional fascinating implications for the flow or motion of energy. The unperturbed flow of energy relies upon a balance of electric and magnetic energy. Electromagnetic waves convey equal amounts of electric and magnetic energy at the speed of light. As that balance is disrupted by the process of interference, the energy slows down. In the limit where either the electric or magnetic fields go to zero, the Poynting vector and the energy flow go to zero. The energy becomes momentarily static.
And yet, the waves continue propagating through each other at the speed of light. How then can the energy associated with the waves come to a stop and catch up? The answer is that the waves exchange energy with each other. The energy in two interfering waves slows down, comes to a rest, and then changes direction.
Consider the destructive interference of two doublet waveforms as shown in the figure below. The figure below (right) shows a 1-D transmission line, but equivalently, these could be plane electromagnetic waves in free space. At time t = 0, the two waves destructively cancel location z = 0. Physicists look at interactions like these in what are called space-time diagrams. The vertical axis denotes time t and the horizontal axis denotes distance z. We can plot the energy density of the two interacting waves using a color scale and plot the energy flow streamlines from the Poynting vector.
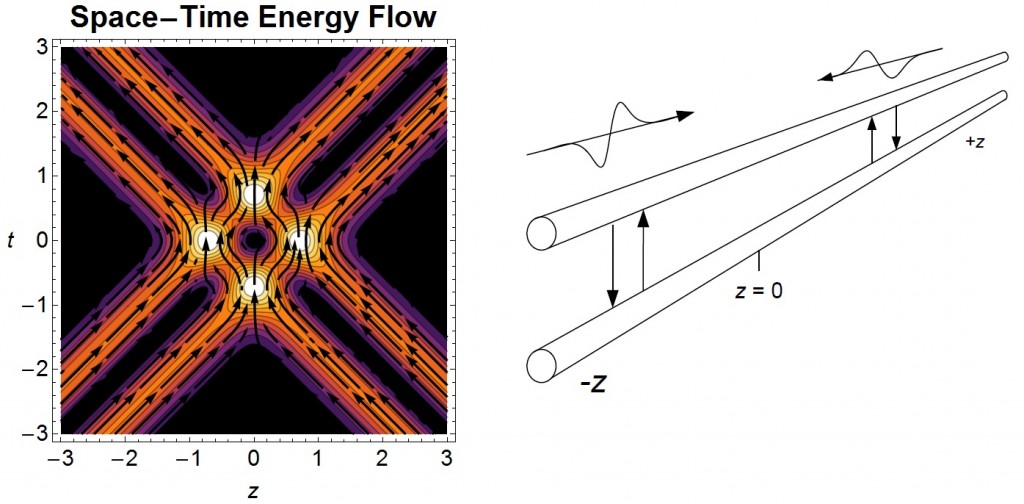
In the negative time portion or bottom of the space-time energy flow diagram (above, left), the two mirror-image doublet waves approach each other. At about t = -1, the leading edges interfere constructively yielding an electrostatic concentration of energy. At t = 0, the two waves superimpose destructively, yielding a pair of magnetostatic nodes of energy. Then as the waves continue moving past each other, their trailing edges superimpose destructively at about time t = +1, yielding an electrostatic concentration of energy. At each of these two electrostatic and two magnetostatic nodes, the energy comes momentarily to a rest before changing direction.
A few qualitative features are clear from this plot.

Pure EM waves have a balance of electric and magnetic energy. A pure EM wave moving in isolation in free space exhibits a balance of electromagnetic energy – half electric energy and half magnetic energy. Wave interference upsets this balance and slows down energy flow. In the limit of constructive or destructive interference, the energy becomes purely electric or purely magnetic, respectively, and energy becomes momentarily stationary.
Waves exchange energy. Although waves interpenetrate and pass through each other without any apparent effect, the energy they contain slows down and reflects. At any given moment, there is an energy density associated with each field, electric and magnetic, but from moment to moment it is not necessarily the same energy as waves interact, interfere, and exchange energy.
Energy retains the same spatial order. In the 1-D case, note how the energy retains the same spatial order. For instance, the trailing edge energy of the reverse wave becomes the leading edge energy of the forward wave.
EM energy streams never cross. The fundamental rule of EM energy flow is that the streams never cross. Where it appears as though the streams cross, what really happens is waves interfere with each other, energy stops, bounces or deflects, and changes direction.

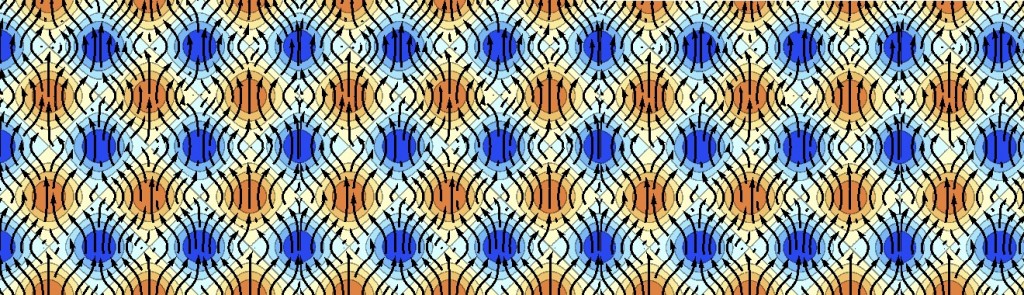
Consider how these ideas play out in the context of harmonic standing waves, an example discussed in detail by Gerald Kaiser. In an ideal harmonic standing wave, equal and opposite waves interfere. At one moment, there are nodes of electrostatic energy along the line, spaced at half-wavelength intervals. A quarter period later, there are nodes of magnetostatic energy spaced a half-wavelength apart, offset by a quarter wavelength. Energy oscillates between electrostatic and magnetostatic nodes, a quarter-wavelength apart in space and a quarter-period later in time. The figure below shows a space time diagram of the oscillation between electrostatic (orange) energy and magnetostatic (blue) energy.
Strong Versus Weak Superposition
Superposition is the principle that the net effect or response at a given place and time is due to the sum of the responses that would have happened due to each of the individual causes or stimuli. This very powerful principle holds true for linear physical models in general and for electromagnetics in particular. At any given point in space and time in a particular reference frame, there is a net electric field and a net magnetic field that is due to the sum of all the individual causes or stimuli relevant to the fields at that point and time. The superposition principle allows us to reduce complicated electromagnetic problems to more manageable component pieces. By allowing us to focus on each particular aspect of interest in turn, while ignoring less relevant characteristics of the system, the superposition principle vastly simplifies our investigations and analyses. When we have carved out a particular limited set of causes or stimuli for analysis, do there associated fields, energies, and power have an independent identity or existence apart from the collective superposition?
We may interpret superposition in a couple of ways. According to “strong” superposition, there is only one electric field and one magnetic field. Thus there is one electric energy density at that point and time, one magnetic energy density, and one Poynting vector (flow of power). My analysis relies implicitly on this assumption. We may decompose the net field to consider only some limited subset of causes and effects relevant to solving a particular problem at hand, but the remaining components are still there. From a weak superposition perspective on the other hand, one might argue the contrary – that while the net energy flow is zero, this is because there are equal and opposite flows of energy that retain their own independent identities.
So why favor strong superposition? Consider the principle of parsimony (or Occam’s Razor) – among competing equivalent hypotheses, one should favor the simpler hypothesis. While it is always valid to decompose the net field into arbitrarily many components, which particular set of components do we identify as being fundamental? There are arbitrarily many ways to decompose and rearrange the components. Which is the correct arrangement; which decomposition accurately describes the underlying reality?
Implications for Macroscopic Energy Flow
The superposition principle allows us to reduce complicated electromagnetic problems to more manageable component pieces. By allowing us to focus on each particular aspect of interest in turn, while ignoring less relevant characteristics of the system, the superposition principle vastly simplifies our investigations and analysis.
However, the great benefit of superposition leads to a similarly great misconception – the notion that aspects of a system not relevant to an analysis are not relevant to understanding the system as a whole. Superposition allows us to ignore other aspects of reality as irrelevant to a particular problem. While those other aspects may be safely ignored in the narrow context of a particular calculation, they are nevertheless present in reality. To understand the big picture of an electromagnetic system, one must step back and take a look at how all the components fit together to contribute to how the system as a whole really works.
Consider a typical electromagnetic calculation involving a cell phone link. We envision the problem as involving a direct propagation of energy from the phone to the tower. We might also consider the effect of one or more alternate propagation paths, for example, a signal reflecting off the ground. For purposes of a detailed calculation we might look at near-field effects close to the transmit and receive antennas. But most of the problem is the essentially far-field calculation of understanding how the cell phone energy propagates through free space from phone to the tower.
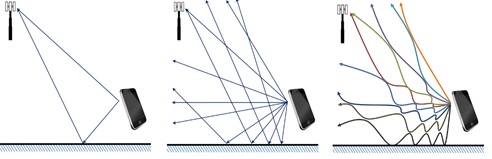
While the above picture (left) may lead to a correct calculation, the physical depiction misleads. In reality, signals and energy propagate from the phone in all directions, setting up the complicated interference pattern of signals in the center figure. However, this “optical” picture of the situation similarly misleads. Applying the principle “don’t cross the streams,” leads to the more correct physical picture above (right). Each point at which rays “intersect” actually denote mutual recoil or reflection of energy. The energy trajectory from the phone to the tower does not involve the ground at all, only myriad meanders as the energy bounces off and interacts with other energy in the system. Although signals and fields propagate at the speed of light, the energy propagates at a more leisurely pace depending on the amount and extent of the delays caused by the overall standing wave environment.
The depiction of the figure to the right presents a gross oversimplification. First, the actual standing wave reflections and reverberations of energy occur on a scale on the order of a half-wavelength – too small for a coherent presentation in the figure. These actually become significant for frequencies low enough and wavelengths long enough that a half-wavelength becomes a significant distance. Second, we have taken advantage of the superposition principle to focus only on the cell phone signals. However, the cell phone link is an infinitesimal part of the big picture of what’s really going on. The dominant energy flow during daylight hours is likely to be the approximately 1kW/m2 flux of energy from sun light. Later in the day as the region reaches thermal equilibrium, there will be an equal and opposite flux of infrared energy. At night, the infrared radiation of the earth dominates, supplemented by everything from the earth’s magnetostatic and electrostatic fields, to lighting impulses, and high power broadcast signals.
In all likelihood, none of the energy actually radiated from the phone ever reaches the tower. Instead, the energy originating from the phone quickly loses itself in the collective superposition of energy near the phone. The fields and waves from the phone send a faint ripple through the collective superposition of electromagnetic region, slightly perturbing the energy associated with the dominant standing waves. In the vicinity of the tower, a small fraction of the local energy decouples from the superposition and interacts with the receive antenna on the tower.
The far-field representation of electromagnetics is a useful analytic approach to solve a broad range of physical problems. As a physical model of reality however, the far-field representation is only valid in a context in which there is one dominant energy flow. Examples might include the propagation of sunlight within the solar system, the flow of energy near a high power transmitter, or the behavior of a transmitter at power levels well above thermal in an anechoic chamber. In most other cases, we apply superposition to focus our attention on the function and behavior of some small fraction of the total fields and energy. Our analysis is correct and meaningful, but it ignores everything else that goes on, co-existing with the problem of interest. The rest of the collective superposition of fields and energy is still out there, its behavior dominated by the largest fields and energy flows in the environment.
When we shift our attention to examine the big picture, some truly surprising implications become obvious. The dominant flux of electromagnetic energy in our solar system is solar radiation. Nothing else even comes close. Imagine light from a distant star approaching Earth. At some point, light years away, the solar fields and energy flow dominate those of the distant star. The light waves from the distant star continue propagating in toward earth, but as they do so, they nudge or perturb the vastly greater energy flow associated with solar radiation.
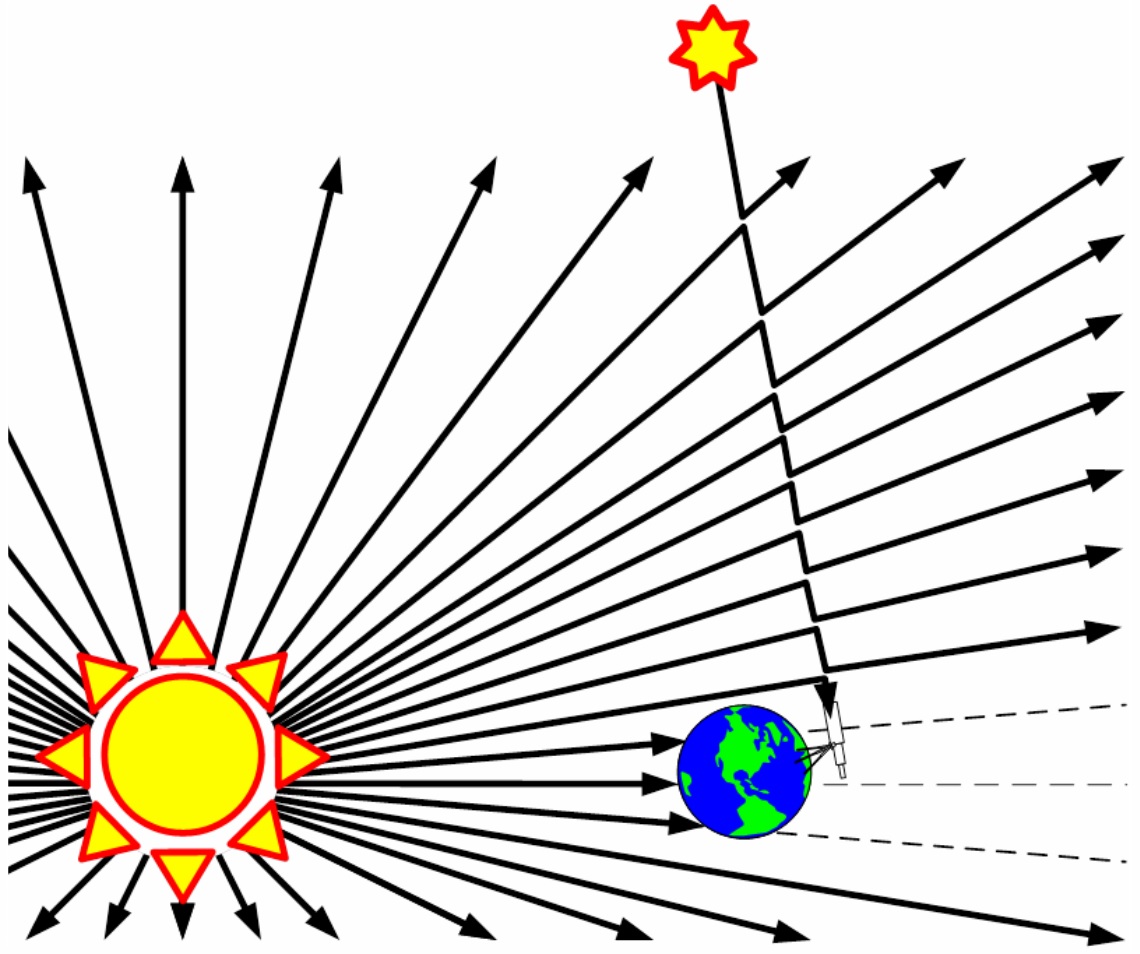
The EM waves propagate into the solar system and are detected by an observer on Earth who sees the distant star. But the actual energy now associated with those fields had its origin in the sun or other closer sources. In all likelihood, although we perceive fields and waves from distant sources all the time, we may never have detected EM energy originating from outside our solar system. The figure above provides a qualitative 2-D diagram of this phenomenon.
A Paradigm Shift
A profound and surprising change in perspective is hardly unprecedented in physics, let alone in electromagnetics. Back in the nineteenth century, there was speculation regarding how electrical current worked in a simple circuit (figure a, below). For more than fifty years, electricians had been multiplying voltage and current to obtain the power dissipated in a resistor. To the extent practitioners thought in terms of a physical model, they relied upon an analogy to plumbing (figure b, below). A battery is like a pump, forcing an electric current through wires like a fluid flowing through a pipe. A resistor is analogous to a turbine, converting the flow into heat energy. Then, along came an unemployed telegrapher (Heaviside) and a professor (Poynting) to claim that instead the correct approach was to evaluate and integrate the Poynting flux over the surface of the resistor. In the Poynting-Heaviside theory, energy flows through the space around the wires, not in the wires (figure c, below). One can appreciate the degree of skepticism directed at Poynting, Heaviside, and the other Maxwellians.
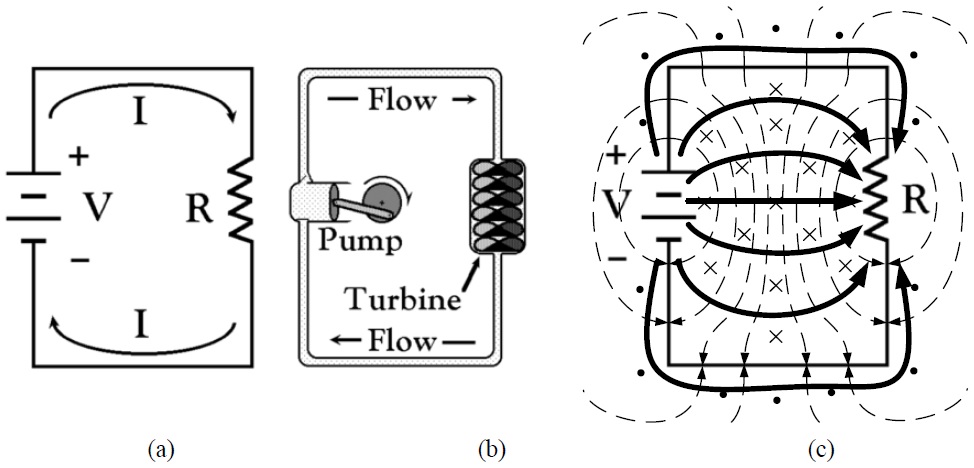
However, advances in AC electronics soon demonstrated the merits of Poynting and Heaviside’s counterintuitive perspective. The resistance of a wire increases with increasing frequency as current concentrates closer to the surface of a wire. The Poynting-Heaviside theory offers a natural explanation: since energy propagates into the wire from the surrounding space, at high frequencies the electric fields of one polarity have less time to permeate into the conductors before the polarity reverses and the process starts over with fields of the opposite polarity.
To recapitulate, applying strong superposition to conventional Maxwellian EM and energy flow leads to some startling and long overlooked conclusions about how electromagnetics behaves. EM fields and waves propagate through each other all the time. Little EM waves pass through much larger EM waves with no discernible impact on each other. But when we look at the energy flows associated with these waves, we discover that they trade or exchange energy with each other all the time. The mean free path of EM energy tends to be relatively short. The drift velocity of EM energy tends to be less than the speed of light – much less than the speed of light in regions at thermal equilibrium. In fact, the behavior of EM energy in free space is a bit analogous to the flow of current in a wire. Just as the fields guide, nudge, and perturb the charges that give rise to currents, so also do fields propagating in free space guide, nudge, and perturb the associated energy.
To be clear – this perspective does not require treating energy as some kind of material substance. Rather the goal is to understand and trace the flow of energy in free space with the goal of understanding the underlying processes and mechanisms.
Application of energy flow to simple circuits led to useful concepts like skin depth and AC resistance. What similar lessons might be learned from strong superposition and energy flow in free space? What are the implications of these classical EM conclusions for the microphysics that must ultimately be responsible for this behavior? What can EM tell us about QM?
What About QM?
Many physicists adopt a pragmatic point-of-view with respect to their calculations. They adhere to a policy of “shut up and calculate” – see Luboš Motl’s blog post for details. The ultimate value of a theory is whether it can provide testable insights and conclusions.
First, do photons interact with each other at everyday energy levels? The conventional thinking, for instance, would be that the cell phone described above radiates its microwave photons. These microwave photons that pass unperturbed through the larger fluxes of solar and infrared photons zipping through the same propagation environment. This would be the physical process associated with weak superposition thinking. The figure below (left) depicts this conventional wisdom. How then can photons give rise to standing waves with their localized concentrations of electrostatic and magnetostatic energy? These are well established, testable facts of EM, confirmed in every day RF practice. How do these clouds of non-interacting photons pass through each other and by virtue of their non-interaction nevertheless manage to give rise to the macroscopic behavior of standing waves? Action arising from non-interaction? To paraphrase Newton, “this is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it.”
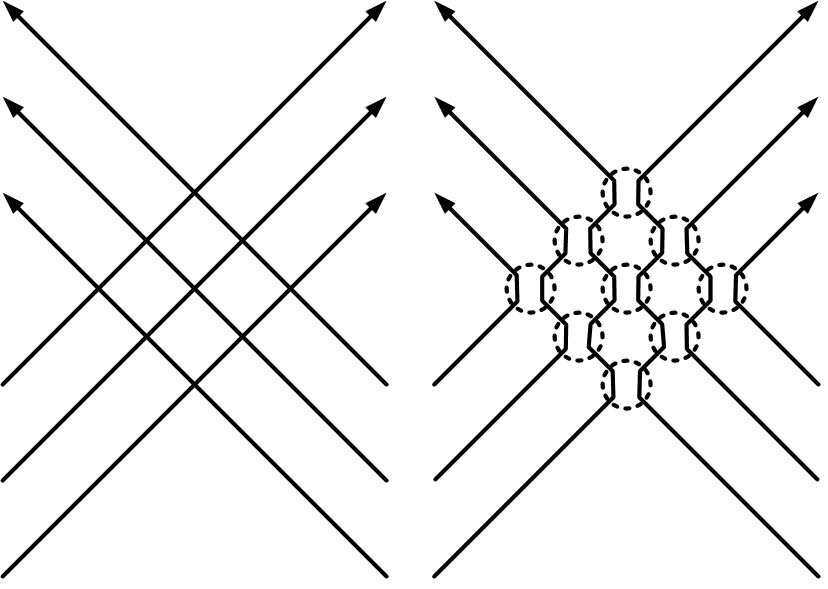
A much more reasonable model would be to accept that the macroscopic behavior of standing waves follows from the microscopic behavior of photons. As two propagating photons – each with a balance of electric and magnetic energy – interfere, they give rise to one or more virtual photons with electrostatic or magnetostatic fields and energy. As they decouple, they once again condense into propagating photons and continue on their way until the next interaction. These interactions may be perfectly elastic collisions (as shown above) if the photon frequencies are identical, or portions of the energy may be exchanged if the photons are characterized by different frequencies.
Second, how to test the photon-interaction hypothesis? This hypothesis has no impact whatsoever on observable behavior of photons in long distance propagation. Absent a clever way to tag and track energy, there is no way to tell whether the energy that departed a source is the same energy received at a detector. The implications of this hypothesis may be observed only in the actual process of interference. The positive result from the experiment of Magyar and Mandel (described in the link above) is already encouraging. A repeat of Magyar’s and Mandel’s experiment with the challenging difference of employing photon sources on different and distinct frequencies would provide additional evidence.
Stepping back a moment, consider the big picture. Applying strong superposition to classical EM yields a picture in which fields guide energy. Fields and waves propagate from point to point as described by Maxwell’s equations, but under conditions of interference, these fields and waves exchange energy with each other. At any given point there is an energy density associated with the fields and proportional to the square of the field intensity, but from moment to moment it’s not the same energy associated with the same wave. Energy and fields are only loosely coupled from this classical point of view. How then do we progress to the quantum limit and obtain quantization? We know from a century of theory that the energy is quantized, but are the fields themselves? As the fields get weaker and weaker, we know that their energy becomes quantized in photons. What about the fields? If the fields were strongly coupled to photons, then we might imagine a transition from classical to quantum in which the field lines collapse and are quantized in synchronicity with the energy. Gauss’ Law tells us that radiation fields must form closed loops. This would suggest that on the quantum level, photons would have small field loops that would have to exhibit longitudinal polarization in addition to the usual two transverse polarizations – a conclusion that ought to be testable (Note: I would expect a negative result, since I suspect this is not what actually happens). On the macroscopic level, the longitudinal components would cancel under the superposition of any significant number of photons, giving rise to the two usually observed transverse polarization states.
If we accept instead that energy and fields are only loosely coupled, this leads to an alternate point of view. In the quantum limit, the fields become too weak to reliably nudge or perturb the underlying electromagnetic energy, distributing it everywhere according to the square of the field intensity. The weak fields still pervade the propagation environment and still interfere with each other classically. Incident on two closely spaced slits, the fields propagate through the two slits and generate an interference pattern. The fields then guide or pilot an individual photon through one slit or the other to a detector along a trajectory that takes into account the interference behavior of the fields and waves. Thus, the classical picture of EM energy flow looks remarkably like the pilot-wave model of QM.
The pilot wave perspective of quantum mechanics, pioneered by Louis deBroglie (1892-1987) and David Bohm (1917-1992), treats individual particles or photons as guided by quantum waves along discrete trajectories [see T. Norsen]. For photons, these trajectories are essentially the electromagnetic energy flow streamlines [see M. Davidovic, et al]. Recently, Kocsis et al observed average trajectories of single photons in a two-slit interferometer and confirmed that a weak measurement of photons enables the determination of photon trajectories [see S. Kocsis et al]. These quantum mechanical measurements may also be interpreted as measurements of the classical Poynting vector field [see K.Y. Bliokh, et al].
Summary and Conclusion
Dirac’s argument for the non-interference of photons does not take into account the mutual interactions of electric and magnetic fields under interference. Applying strong superposition to classical EM energy flow leads to surprising and counter-intuitive conclusions about the large scale behavior of energy flow in electromagnetic systems in particular and reality in general.
QM may be more fundamental than EM, but QM must also explain and be consistent with the observed and experimentally tested facts of EM. Standing waves exist. There are concentrations of electrostatic and magnetostatic energy arising in every interference of EM waves. QM needs an explanation and model for how they work. Action from non-interaction is not an acceptable theory. The classical EM theory of energy flow combined with strong superposition offers a reasonable answer.
Interested in learning more?
- Hans G. Schantz, “On the Superposition and Elastic Recoil of Electromagnetic Waves,” FERMAT, Vol. 4, No. 2, July-August 2014 [ART-2014-Vol4-Jul_Aug-002]. See also http://arxiv.org/abs/1407.1800.
- Hans G. Schantz, “On Energy Flow in Standing Waves,” 2014 Antenna Applications Conference, Allerton Park, Illinois, September 25, 2014. [Video].
- Hans G. Schantz, The Art and Science of UWB Antennas, 2nd ed., Norwood, MA: Artech House 2015.
- Travis Norsen, “The pilot-wave perspective on quantum scattering and tunneling,” American Journal of Physics, Vol. 81 No. 4, April 2013, pp. 258-266.
- M. Davidovic, et al, “Electromagnetic energy flowlines as possible paths of photons,” Phys. Scr. T135, 14009 (2009) [arXiv:0805.3330].
- S. Kocsis et al, “Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer,” Science Vol. 332, 3 June, 2011, pp. 1170-1173.
- K.Y. Bliokh, et al, “Photon trajectories, anomalous velocities and weak measurements: a classical interpretation,” New Journal of Physics, Vol. 15, (2013), pp. 1-17.

5 thoughts on “Dirac’s Big Mistake: What EM Tells Us About QM”
What are the chances you and Carver Mead can do a road trip together? Need any roadies? Groupies?
Carver Mead does an excellent job explaining the – I’d call it “transactionalist” approach to EM. I had the opportunity to discuss the Wheeler-Feynman time-symmetric EM theory with Wheeler himself when I was in grad school. I never really got it until reading Carver Mead’s treatment. Your proposed road trip would make for an interesting opportunity for discussion!
Any role here for Weber’s electrodynamics? ( viz AKT Assis, e.g.)
Thanks for this work.
Weber’s electromagnetics is more akin to the kind of action-at-a-distance theories Faraday was reacting against when he pioneered field theory. It may be mathematically equivalent, but I find fields with their promise of locality and causality a more appealing model.
Thank-you Hans for an informative and well explained blog-post.
Years ago, I was calculating and plotting 2d cross sections of static magnetic fields, and got to wondering if the original fields remained independent entities, and lo, now I can give this direction of thinking the name of “weak superposition”.
Your cautionary reminder to remember to take into account the whole EM environment, along with your Space-energy diagrams got me wondering about the complexity of our local EM environment.
In considering the general background energy flux at in our everyday EM environment, you included earth’s static magnetic field. But, in my imagination, the earth’s magnetic field is a roiling, pulsing and rather dynamic. Further, wouldn’t one also included the sun’s magnetic field, all interacting in the strong super-positional manner you described?
My question is, have I got this wrong – is the background magnetic component a little less lively than I imagined, and if not, what kind of affect does this have on local EM interactions?