Maxwell first published his famous equations describing electricity and magnetic one hundred fifty years ago this month. In honor of the anniversary, ÆtherCzar will discuss some interesting and not always appreciated aspects of Maxwell’s Equations. First, is radiation divergenceless?
“Divergence” is a mathematical property of fields, measuring the extent to which they radiate from a source or terminate in a sink. In the context of electricity and magnetism, magnetic fields are divergenceless – they always form closed loops with no source or sink. Equivalently, there are no no magnetic charges or “monopoles” where magnetic fields begin or end.
Electric fields do exhibit divergence. Electric fields begin at positive charges and terminate on negative charges (under some, but not all, circumstances). One of Maxwell’s Equations, called “Gauss’ Law for Electricity,” explains that the divergence of the electric field vector (E) is equal to the charge density (ρ in C/m3) divided by a proportionality constant called the permitivity of free space (ε0 = 8.85… × 10−12 F/m):
In a source-free or charge-free region, the charge density is ρ = 0, and Gauss’ Law for electricity becomes, simply:
The radiation field of a small harmonic electric dipole source is:
where p0 is the electric dipole moment, ω = 2 π f is the angular frequency, k = 2 π / λ is the wave number, c is the speed of light, r is the radial distance, and θ is the angle with respect to the axis of the dipole source. Taking the divergence of the radiation field yields:
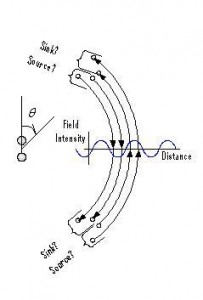
The divergence of the radiation field term is NOT zero as would be expected from Gauss’s Law for a source-free region. This mathematical result may be easily understood by drawing a diagram of the radiation field. The radiation field lies entirely in the θ direction. Most intense at θ = 90 deg, the field intensity decreases and eventually vanishes as θ approaches θ = 0 deg or θ = 180 deg. Where do the field lines go? Field lines must begin and end on electric charges. Either the electromagnetic radiation described above carries with it some sort of charge distribution as it propagates through free space, or, at the very least, it is not a complete and valid solution to Maxwell’s equations.
One might argue (with considerable justice) that since this nonzero divergence goes as the inverse square of distance (as 1/r2), the error becomes increasingly negligible at large distances from the source. But before dismissing this minor anomaly out of hand as an inconsequential error in the radiation approximation, consider what would be required to remedy the discrepancy.
Suppose we were to add an additional term to the radiation field to create an alternate expression for the radiation:
Then, evaluating for the divergence yields:
where again the wave number is k = w /c. This alternate expression for the radiation now satisfies Gauss’s Law.
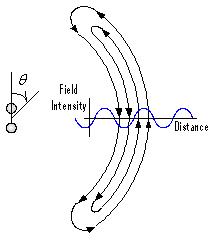
The previous mathematical example probes the fundamental difference between bound (static or reactive) fields and unbound (radiation) fields. An electric field is bound when it begins and ends on an electric charge. The positive charge where a field line begins is a “source,” and the negative charge where a field line ends is a “sink.” Unbound or radiation fields, on the other hand, form a closed loop with neither source nor sink. The extra term in the alternate expression for the radiation field above is needed to close the loop. The figure illustrates this point for a particular cycle of a harmonic electric dipole.
For an alternate view, see Daniele Funaro’s Electromagnetism And The Structure Of Matter. Funaro argues that all non-trivial electromagnetic waves exhibit regions in which the divergence is non-zero. I do not believe this is correct, as witness the above example.
Updated April 5: Please see Prof. Funaro’s comment and my reply below.
The classical “radiation field” falls off as 1/r, and this is the dominant term as r → ∞. Why then do we have any business considering the radial field term that falls off as 1/r2? Consider the integral formulation of Gauss’ Law, as applied to a Gaussian box in spherical components, co-moving with the radiation field at a radial distance r so that r = c (t – to) where “c” is the speed of light, “t” is time, and “to” is an arbitrary starting time. The electric flux, i.e. the product of the normal component of the electric field and the surface area averaged over the closed surface must be zero for a source free region.
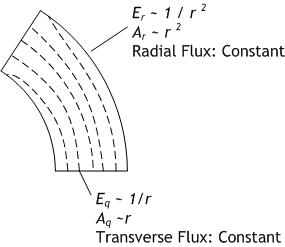
Suppose the box has six surfaces, two surfaces each of constant r, constant θ, and constant φ. The surfaces of constant r have area: r2 sinθ Δφ Δθ. The surfaces of constant θ have area: r sinθ Δφ Δr. The surfaces of constant φ have area r sinθ Δφ Δr, but these can be ignored since Eφ = 0. The flux due to the transverse field component is constant because the transverse E-field is inversely proportional to range (Eθ ~ 1/r) and the surfaces of constant θ have area proportional to range (Aθ ~ r). Similarly, the flux due to the radial field component is constant, because even though the radial E-field is inversely proportional to range squared (Er ~ 1/r2), the surfaces of constant r have area proportional to range squared (Ar ~ r2).
The traditional approximation of radiation fields with inverse range dependance (Erad ~ 1/r) is just that: an approximation. An exact evaluation of divergence of the radiation field requires use of the radial field component with its inverse range square dependance. While this term is negligible in calculating the net field, it is not negligible in calculating the divergence. Without the radial field component, Gauss’ Law will not be exactly satisfied for radiation fields.
The interesting conclusion is that even arbitrarily far away from the source, in the distant radiation zone, a full and physically correct understanding of radiation compliant with Maxwell’s Laws requires the use of what has traditionally been dismissed as a negligible near-field term.
Note: this blog post contains material originally presented in my book, The Art and Science of Ultrawideband Antennas, (Artech House, 2005) pp. 131-133.
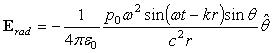
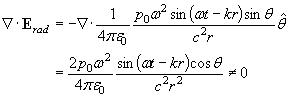
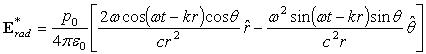
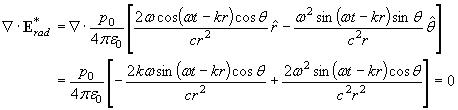




3 thoughts on “Is Radiation Divergenceless?”
Dear Hans,
I think you missed some crucial passages in my dissertation.
I never claimed that ‘all non-trivial electromagnetic waves exhibit
regions in which the divergence is non-zero’. As a matter of fact
there are families of solutions that actually satisfy the divergence
zero condition in full (as also reported in my book on p.16 or
p.133 for gamma_0=0).
As you point out it is possible to built whole regions where one can
locally enforce all Maxwell’s equations. The question is what happens
globally and how is the evolving behavior of the entire wave. Then one
starts having troubles, since there are many non convincing facts about
the way Maxwellian waves develop, as detailed in my book and successive
other papers (see arXiv).
As I argued in the book, my reasonings may be partially uninteresting
when applied to antenna propagation, but starts to be fundamental when
one looks for solitary waves. Finding out model equations that, without
altering the quality of Maxwell’s equations, offer an extended space of
solutions is an important achievement that may open new links between
classical and quantum physics.
Remaining on antenna propagation the theory might explain how the near-field
behaves (recall that due to currents the divergence of the electric field is
not zero on the conductor, so it might be nonzero in the immediate
neighborhood) and possibly help to devise new high-directivity tools.
Daniele Funaro