Remembering John Archibald Wheeler

Saturday July 9 marks the centennial of John Archibald Wheeler’s birth. Wheeler pioneered the theory of nuclear fission along with Niels Bohr. He contributed to the Manhattan Project during the Second World War. Afterward, he led a revival of general relativity theory including coining such memorable terms as “wormholes” and “black holes.”  Wheeler also placed great importance on teaching and mentoring young students. This post shares some personal recollections and remembrances of a recipient of Wheeler’s mentoring.

Magic Bubble Nuclei

As a first year graduate student in physics at the University of Texas at Austin in 1990, I faced a dilemma. I liked physics in general, but I wasn’t particularly passionate about any specific area. I read voraciously books by and about physicists. I tried to identify interesting aspects of physics worth researching further. One passage in George Gamow’s The Great Physicists From Galileo to Einstein caught my attention:

It was shown, however, by the Princeton physicist, John Wheeler, that nuclear fluid may not necessarily exist in the form of little spheres but can, in principle, assume different shapes. The point is, in that case there exist, apart from the forces of nuclear cohesion, also the Coulomb repulsive forces between the positive charges of protons. Wheeler has shown in an unpublished paper that the existence of these repulsive forces permits atomic fluid to assume the shape of a doughnut. In fact, in this case, surface tension forces which tend to contract the doughnut into a sphere will be opposed by electric repulsion between the opposite sides of it, and the entire configuration will be perfectly stable. Such doughnut nuclei, which would be considerably larger than those of uranium, having an atomic weight of many thousands, will be surrounded by electrons which would move close to their surface along trajectories similar to the wiring of a circular electromagnet. Such doughnut nuclei do not exist in nature, and it is hard to believe that they could be manufactured in the future by the most skilled nuclear physicist. But if they could be made, points out Wheeler, one could use them as links to make long chains. the thread made of such nuclear chains would be extremely strong, and, being as thin as cobweb, would hold the weight of a battleship.

I had heard of John Wheeler. My undergraduate course in relativity was taught using his book, Spacetime Physics (co-authored by Edwin F. Taylor). And I had noticed that he was listed as an emeritus member of the U.T. physics faculty. I sent him a note asking for a copy of his unpublished work on toroidal nuclei. Not only did send me more information, he graciously asked if I would like to work on the subject. I accepted eagerly.

Wheeler served as co-adviser for my doctoral candidacy research along with Austin Gleeson. The subject of my work was exotic nuclear geometries like toroids (doughnuts) and bubbles. I further had the good fortune to receive an appointment to the Lawrence Livermore National Laboratory for the summer of 1991, where I worked under the direction of Mort Weiss and French nuclear physicist Paul Bonche. Weiss (now retired) is an expert in an exotic area of nuclear theory known as shape isomers.

Certain atomic nuclei can exist in deformed shapes, even transitioning from a deformed state to a more symmetric state. In principle, these nuclear shape isomers could store enormous amounts of energy. This led to considerable speculation that nuclear shape isomers could provide a high-density energy storage system with performance far beyond conventional batteries. Others theorized that nuclear shape isomers could be the basis of new weapons systems intermediate between conventional chemical explosives and nuclear weapons in which a golf-ball-sized lump of material would be the equivalent of ten tons of high explosives. The hype far exceeded the reality, however. Sharon Weinberger’s excellent book Imaginary Weapons: A Journey Through the Pentagon’s Scientific Underworld, explains these far-fetched claims and how they captured the imaginations of defense researchers despite considerable scientific skepticism and opposition.

My work was much more mundane, although ultimately even more unrealistic. Under the guidance of Weiss and Bonche, I learned how to use and modify Bonche’s spherically symmetric “Hartree-Fock” computer code to investigate the possibility of “bubble” nuclei. This approach let me focus my investigation on “magic” bubble nuclei. Nobel gases are particularly stable because they have exactly the right number of electrons to fully occupy the available atomic orbitals. Electrons may be added to or removed from a closed shell only with great difficulty. Similarly, nuclei with just the “magic” number of protons and neutrons become particularly stable. Since nuclei larger than lead (Pb-208) are unstable, seeking magic nuclei holds out hope that they might be stable enough not to immediately decay away. In parallel with my work on the Hartree-Fock code, I followed Wheeler’s lead in applying the “liquid drop” model of nuclear matter to the problem of bubble nuclei. The results I obtained over the summer seemed quite promising. For instance, I found that for nuclei with atomic number greater than about A = 768, the bubble configuration becomes energetically favored. Results from the Hartree-Fock code roughly aligned. The code predicted Z = 272, A = 914 (for instance) would be a doubly magic bubble nucleus. On the strength of these results I passed my doctoral candidacy exam in the Fall of 1991. The stress and pressure of completing what was normally a two year process in only a year and a half left me so weakened that I caught a serious case of pneumonia requiring a couple weeks of hospitalization.

Ash From Splash

When I recovered, I planned out the course of my research with Wheeler and Gleeson. Of course, the specifics of my doctoral candidacy work were extremely far-fetched. It’s debatable whether super-heavy nuclei as “small” as A ~300 actually exist in anything approaching a stable state. My A ~ 914 predictions were so detached from reality as to be virtually meaningless. However, the work I did had potential value in the context of “nucleosynthesis,” or the processes by which the heavy elements form. One theory (r-process nucleosynthesis) holds that smaller atoms are rapidly bombarded by neutrons during supernovas. They collect neutrons more quickly than the nuclei decay, thus building up the distribution of the heavy elements. Wheeler wanted me to examine a different theory: that the heavy radioactive elements (the “still warm ashes of creation” in Weisskopf’s colorful phrase) were formed from the “splash” of nuclear fluid in such events as the tidal disruption of neutron stars. With his gift for vivid, descriptive labels, Wheeler dubbed the project: “Ash from Splash.” Wheeler was entranced with the high speed photography of Harold Edgerton. The parallels between the transient nature of a drop of water and the behavior of nuclear matter inspired his work on fission and exotic nuclear geometries. At some point, Wheeler commissioned the following line drawing which I believe he said was copied from or inspired by an Edgerton photograph.

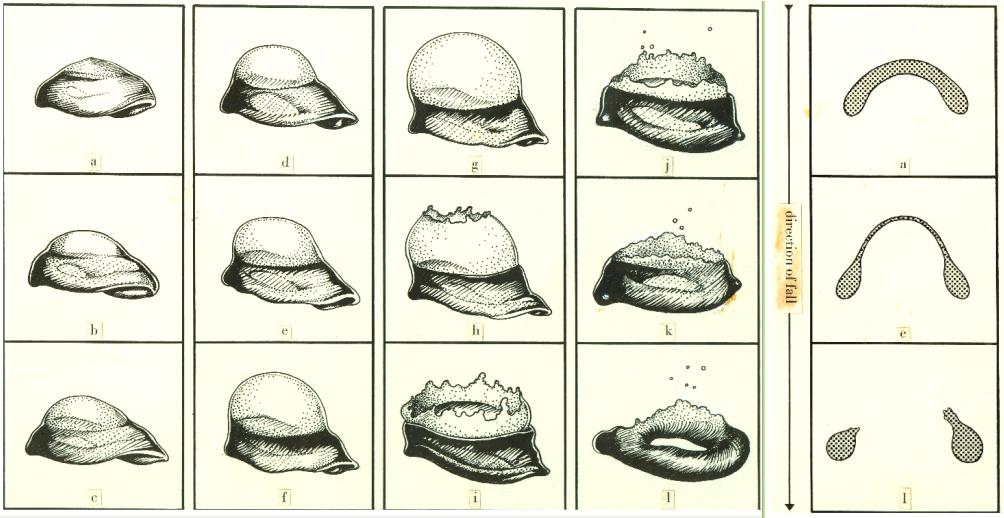
I have lengthy notes from a discussion with Wheeler on April 14, 1992. We started off discussing technical matters related to my proposed dissertation work, like supernovae and  r-process nucleosynthesis, but the subject matter wandered to monopoles, Lamb shift, and meson theory. I had read about Wheeler’s opposition to including parapsychology in the AAAS as described by Martin Gardner (see Science: Good, Bad and Bogus, pp. 185-206). He more or less reiterated Gardner’s account of the controversy. We also talked at length about his views on observer participation in physical reality. Wheeler’s thinking was influenced by such sources as the monism of Leibnitz and particularly by Bohr’s notion of “complementarity.” Wheeler explained the concept of “it from bit,” the idea that information is fundamental, that all physical things arise from simple “bits” of information. I was a bit overwhelmed by it all.

Still, I pressed on for the next year getting deeper into nuclear matter theory, but by the Summer of 1993, I was feeling seriously burned out. I’d developed a nuclear matter model with a couple dozen somewhat arbitrarily defined input parameters trying to evaluate it against the few actual observed parameters of neutron stars. I realized I could fit virtually anything with my model and there was no way to determine my inputs with any specificity. Frustrated, I gave up on nuclear matter theory.

A Scholar and a Gentleman

I realized that I needed closer guidance to make headway and avoid wasting time. And I was frustrated with nuclear matter theory and ready for a change. In the Fall of 1993, I began working with George Sudarshan on studying gravitational energy in the context of general relativity. In March 1994, Sudarshan made a brilliant suggestion that changed the course of my career and my life. Why not approach the problem of gravitational energy by starting with how electromagnetic energy works?  Sudarshan claimed that the Poynting vector (which is supposed to describe the flow of electromagnetic energy) only works for waves and breaks down for static fields. He challenged me to understand and explain why. I’ve spent the rest of my career trying to answer Sudarshan’s question and apply the results to ultra-wideband antenna design and near-field wireless systems.

Although my work was largely guided by Sudarshan at this point, I took advantage of Wheeler’s infrequent visits to Texas to discuss my work in particular and physics in general. I asked Wheeler about some of the great personalities of physics in an extended and far-reaching discussion on May 12, 1994. Wheeler said he’d never met Planck or Schrodinger, but he had a great deal to say about Heisenberg. He recalled meeting with Heisenberg around Easter of 1935, although he didn’t recall the subject of the conversation. He described the (in)famous 1939 “summer school” in Ann Arbor where Fermi and others tried to dissuade Heisenberg from returning to Germany (see, for instance Thomas Powers’  Heisenberg’s War: The Secret History Of The German Bomb, p. 11-12). Wheeler recalled Heisenberg leaving early for “machine gun practice.” About Fermi, Wheeler said: “He was a real driver,” adding, “he had a very businesslike way of going at things.”

Wheeler was a scientific consultant at the Hanford Nuclear Site where plutonium was produced for the Manhattan project. When the reactor was turned on in September 1944, power quickly died off. Unexpected fission products poisoned the reactor by capturing unexpectedly high levels of neutrons. If the reactor had failed, there would have been insufficient plutonium for the Trinity Test device as well as the Fat Man bomb. Only the uranium-based Little Boy bomb would have been available. Fortunately, the reactor had been over-designed with enough margin to overcome the problem.

Writing in The Making of the Atomic Bomb, Richard Rhodes originally credited Wheeler with having over-designed the plutonium reactor to enable it to continue work despite the unexpected fission products. More recently Rhodes updated his account to place the credit in the hands of DuPont manager Crawford Greenewalt (many thanks to Rhodes for confirming in an e-mail this later version of events). I found this quote from Wheeler in an outstanding 1985 profile which provides details beyond what I have in my notes of our May 1994 discussion:

“The real hero of the story was a DuPont engineer named George Graves. He kept asking questions like ‘What in the hell are fission products?’ Once he got into it, he insisted that instead of the 1,500 fuel tubes we had planned to put in, we should have a margin of error of another 500. Actually we had 2,004. That took a lot of gumption, since it cost a lot of money. But thanks to his foresight it was possible to reload those extra tubes with uranium and give the pile the reactivity it needed to overcome the fission product poison.”

I believe it was also in this May 12, 1994, conversation that I asked Wheeler how he felt about his work on the Manhattan Project and if he had any regrets about it. As best I recall, he answered “My only regret is that we didn’t finish it sooner.” He explained his brother was killed in Italy. If the atomic bomb had been finished earlier, the war could have been ended sooner saving countless lives.

My study of the history of quantum mechanics led me to be a skeptic of the Copenhagen interpretation in general and to reject Wheeler’s “it from bit” concept in particular. I’ve explained my thinking at greater length in “The Philosophic Premises of Quantum Theory,” Part One and Part Two. I also pressed Wheeler about some alternate interpretations of quantum mechanics. Wheeler dismissed the deBroglie-Bohm view of quantum mechanics, calling it “the screwdriver theory of the double slit experiment.” When I asked him to elaborate his objections, Wheeler said “I never really studied into that business and I really should so I can see what’s wrong with it.”

This conversation illustrates what I appreciated most about Wheeler. Although I was a lowly graduate student in profound disagreement with his cherished beliefs, he treated me with the utmost courtesy and respect.  And although he clearly disagreed with the idea I championed (of an objective reality independent of observation underlying quantum mechanics), when I happened to press him beyond the limits of his familiarity, he freely acknowledged his ignorance. Wheeler was the epitome of a scholar and a gentleman.

Causal Surfaces and a Space-Time Description of Radiation

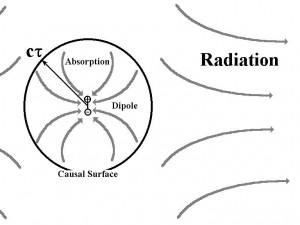
My research progressed quickly. In June 1994, I submitted my first technical paper on electromagnetic energy flow to the American Journal of Physics. The energy flow around an  exponentially decaying dipole has some interesting features that highlight the complex ways in which electromagnetic radiation works. I discovered that there is a spherical shell of radius r = c τ, (where τ is the time constant of the decay)  around the dipole where the magnetic field and thus the Poynting vector are exactly zero. I showed that inside this shell the dipole absorbs energy. All the radiation energy comes from the static field energy stored outside this shell – not from the vicinity of the accelerating charges themselves. I dubbed this a “causal surface,” since it partitions causally separate flows of energy.

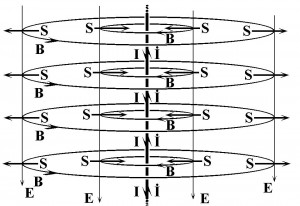
Contrary to Sudarshan’s assertion that the Poynting vector doesn’t apply to or breaks down for static fields, I ran down every alleged puzzle or paradox associated with the Poynting vector and convinced myself that they were all solvable. By this point, I was making great progress toward my doctoral dissertation on electromagnetic energy. Wheeler in particular helped me understand the flow of energy into a resistive wire.

Just as the induction magnetic field follows from application of the right-hand rule to the current, the radiation magnetic field follows from application of the right-hand rule to the change of current vector. When these two vectors oppose, radiation energy separates or tears away from the antenna at the causal surface where the magnetic field is zero. Inside the causal surface, energy is absorbed in ohmic losses.

During the summer of 1995 I worked feverishly to complete my dissertation, reviewing drafts with Sudarshan and my other committee members. I faxed drafts to Wheeler at a store near his summer home on High Island, Maine. I was deeply impressed with the time and effort Wheeler spent not only in his detailed comments and criticisms, but also in treking out to receive the faxed drafts and returning to transmit the marked up copies. I successfully defended my dissertation in August 1995. For me, the highlight was not when I received my doctoral diploma in the graduation ceremony, but rather when Sudarshan, Wheeler, and the other members of my committee were the first to congratulate me as “Doctor” Schantz.

Regrettably, I fell out of touch with Wheeler after my graduation in 1995. However, Wheeler profoundly influenced my spacetime approach to understanding the process of electromagnetic energy flow. Since my causal surfaces denote places where either the electric or magnetic fields go to zero, they are also surfaces of constant phase. When I first plotted the magnetic causal surfaces of an electric dipole on a space-time diagram, I initially thought I had discovered superluminal propagation in near-fields. The magnetic phase initially propagates at infinite velocity before slowing down to the speed of light about a quarter wavelength away. The electric phase behaves in an even more fantastic fashion, propagating backwards in time for the first quarter wavelength before traveling forward in time again. In fact, the electric phase appears to be in two places at the same time. Holy causality!

Understanding the actual energy velocity yields a much more prosaic explanation. A harmonic dipole emits energy for a quarter period. Then for the next quarter period, it absorbs energy. The average energy velocity is strictly bound by the speed of light for all times and ranges. Energy is typically emitted, stored in the reactive fields for a quarter period and then either radiated or reabsorbed by the dipole. The space time energy flow diagram below denotes integrated energy density on the shell of radius “r” by color. Red denotes the highest energy density and purple the lowest. The arrows denote the energy velocity: a vertical arrow means energy is stationary, an arrow at an angle of 45 degrees denotes energy traveling at the speed of light.

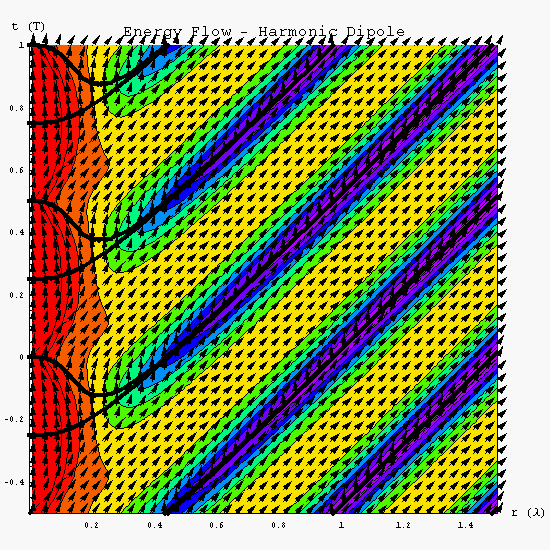
My “discovery” of these phase relationships was actually anticipated by Heinrich Hertz in the 1880s (see Hertz, Electric Waves, (1893) p. 152). However, the subtleties and the potential of this near-field electromagnetic physics have not been generally appreciated. These and other properties of near-field electromagnetics are the basis of innovative real-time location systems available from a company I co-founded: The Q-Track Corporation.

Conclusion

Wheeler was a superb physicist, and an outstanding mentor. I’m grateful for this opportunity to acknowledge my debt to him and say, “thanks!” To learn more about John Archibald Wheeler, I recommend Jeremy Bernstein’s remarkable profile. Wheeler’s autobiography, written with Kenneth W. Ford, is also available: Geons, Black Holes, and Quantum Foam: A Life in Physics.

UPDATE: This obituary by Marcus Chown provides a great summary of Wheeler’s life and career. Chown’s book, The Magic Furnace: The Search for the Origins of Atoms is a truly outstanding and highly readable discussion of nucleosynthesis.

UPDATE (7/11/2011): Also, fixed a couple of typos and formatting problems.